回折の起こる逆格子点の選択

結晶格子と逆格子

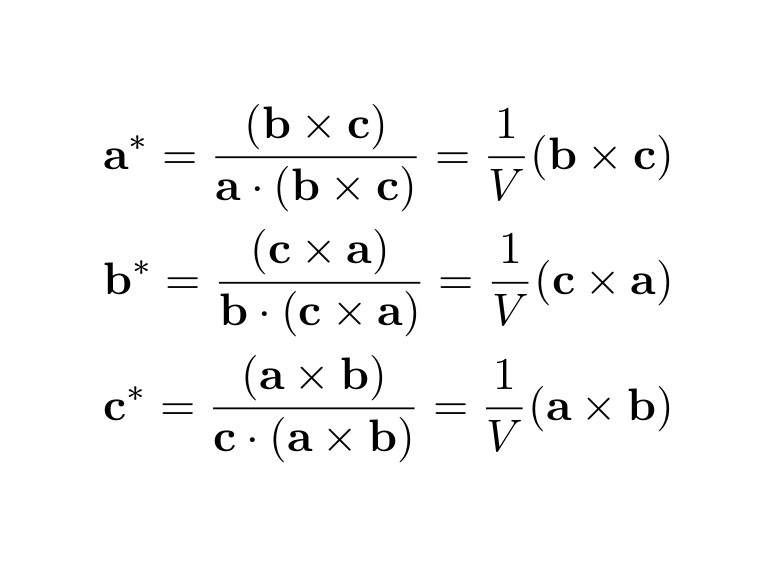
結晶格子と逆格子は互いにフーリエ変換・逆フーリエ変換の関係にある。ベクトルで記述するとそれぞれの関係を簡潔に書くことができる。 単位胞の繰り返し周期を表し結晶格子の底となるベクトルをa，b，cとする。 これらに対する逆格子の底となるベクトルは次のように定義する。

注意　ここでの逆格子ベクトルの定義は結晶学のものである。通常，物理一般ではこれを2π倍したものを逆格子ベクトルとする。

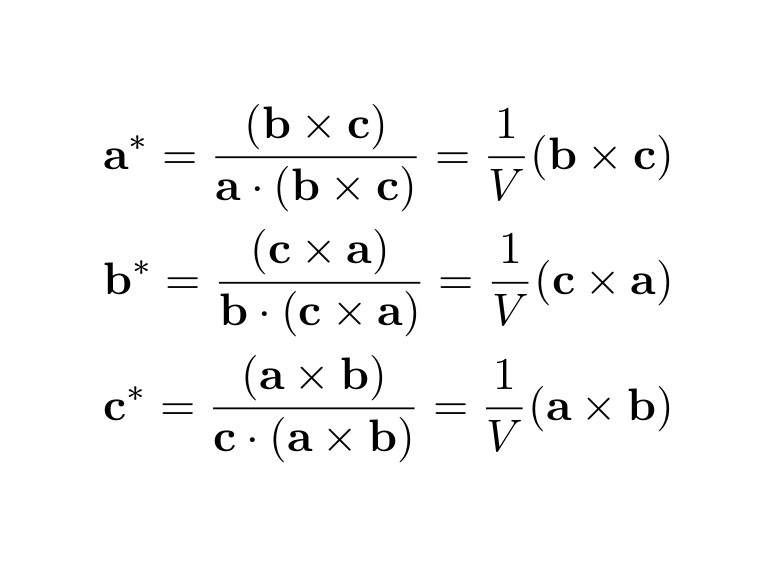
ここでVは単位胞の体積であり，×はベクトルの外積を，⋅が内積を示す。例えば外積b × cの結果はbc平面に垂直にaのある方を向き，大きさがbc面の面積のベクトルになる。そのため，a ⋅ (b × c)は単位胞の体積となる。つまり，a^*，b^*，c^*はそれぞれbc平面（A面），ca平面（B面），ab平面（C面）に垂直であり，大きさはそれぞれA面の間隔の逆数，B面の間隔の逆数，C面の間隔の逆数になっている。

このようにa^*，b^*，c^*を定義すると以下の関係が満たされる。

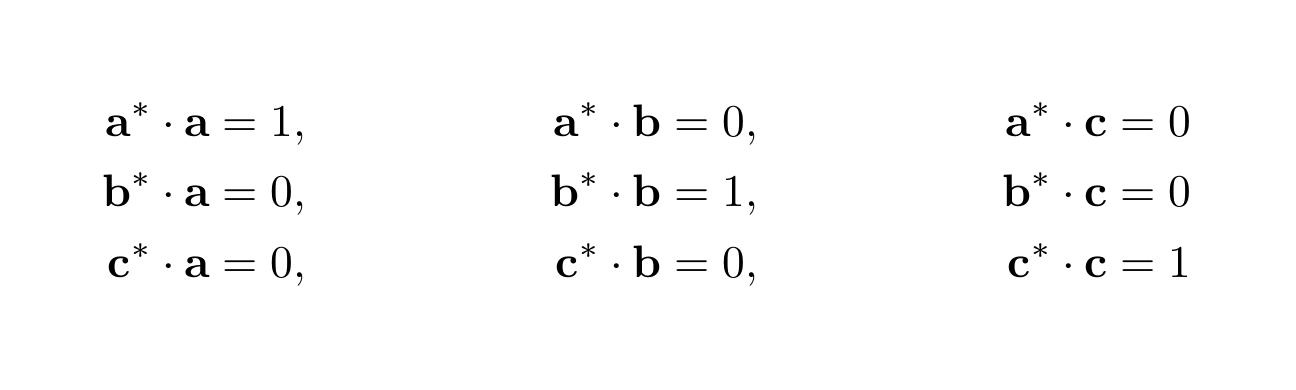
a^*，b^*，c^*は逆空間を張るベクトルとなっており，逆空間中の任意の点を指すベクトルgはu，v，wを実数としてg = u a^* + v b^* + w c^*と表すことができる。u，v，wが整数の時（それぞれh，k，lとしよう）はgは逆格子点を指すが，散乱ベクトルsがそのようなgと一致するとき，すなわち逆格子点を指す（s = h a^* + k b^* + l c^*）ときにラウエ条件が満たされ，回折が起こる。この時，結晶格子のミラー指数h，k，lの面(h k l)に対し，幾何学的にsは垂直であり，その大きさは(h k l)の面間隔の逆数に等しい。

格子点の座標

散乱ベクトルが逆格子点を指すときに回折が起こるので，逆格子点の座標を知る必要がある。 与えられているのは格子定数a，b，c，α，β，γであるので，これを元に実空間と逆空間の3次元中の格子点の座標を計算して求める。具体的にはベクトルa，b，cの指す座標（ベクトルの成分表示）を求め，逆格子の底となるベクトルa^*，b^*，c^*の座標（成分表示）を計算することとなる。

単位胞のa軸をX軸と平行に，b軸をXY平面と平行に，c軸がZ軸の正の方向になるようにとる。 このように置くと，格子ベクトルの成分は格子定数のa，b，c，α，β，γから

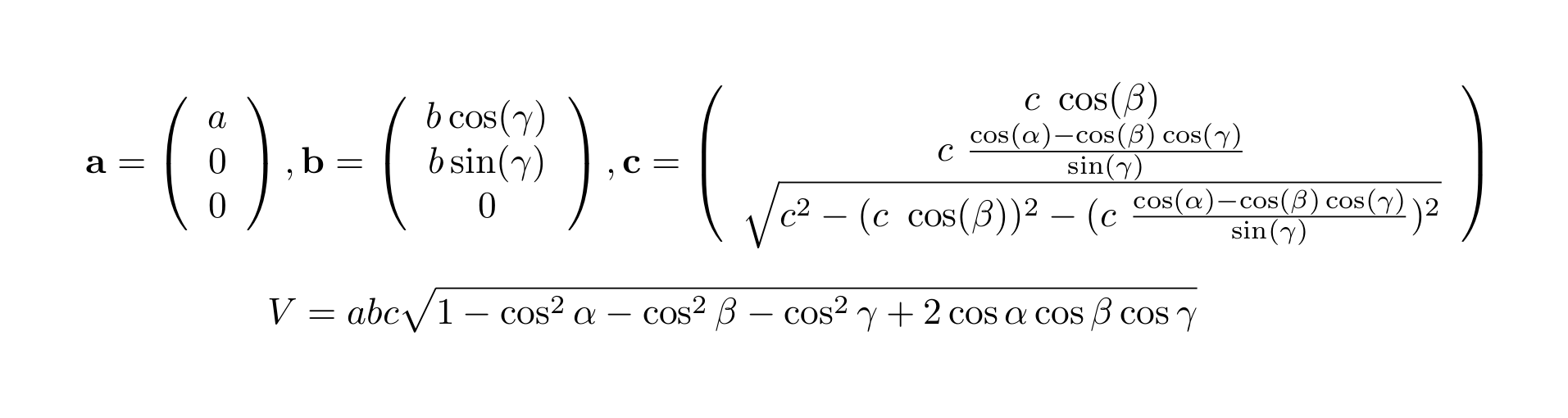
となる。逆格子ベクトルの成分は上にある定義に従って計算する。

座標の回転

一般的に知られる剛体の方位を与えるオイラー角は

1. 剛体とその内部座標(x, y, z)をz軸まわりに角度α回転させ，(x′,y′,z′)とする
2. (x′,y′,z′)をx′軸まわりに角度β回転させ，(x″,y″,z″)とする。
3. (x″,y″,z″)をz″軸まわりに角度γ回転させ，(X, Y, Z)となる。

で示されるα，β，γで与えられる。座標と回転の与え方の関係からintrinsic rotationと呼ぶ（z − x′−z″ rotation）。

今回のプログラムでは，これと同等のものとして外側の固定した座標軸回りに回転させるextrinsic rotationで座標の回転を扱っている。

1. Z軸まわりに角度ϕ回転させる。
2. X軸まわりに角度χ回転させる。
3. Z軸まわりに角度ψ回転させる。

こちらはZ − X − Z rotationである。剛体の方位が等しいときはオイラー角とϕ = γ, χ = β, ψ = αの関係である。

点P(x, y, z)をZ軸まわりに角度ϕ回転させ，P'(x', y', z')とする回転は

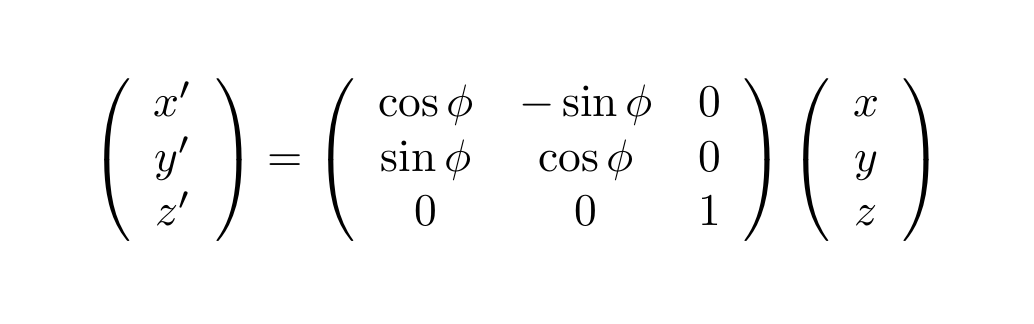
次に点P′(x′,y′,z′)をX軸まわりに角度χ回転させ，P″(x″,y″,z″)とする回転は

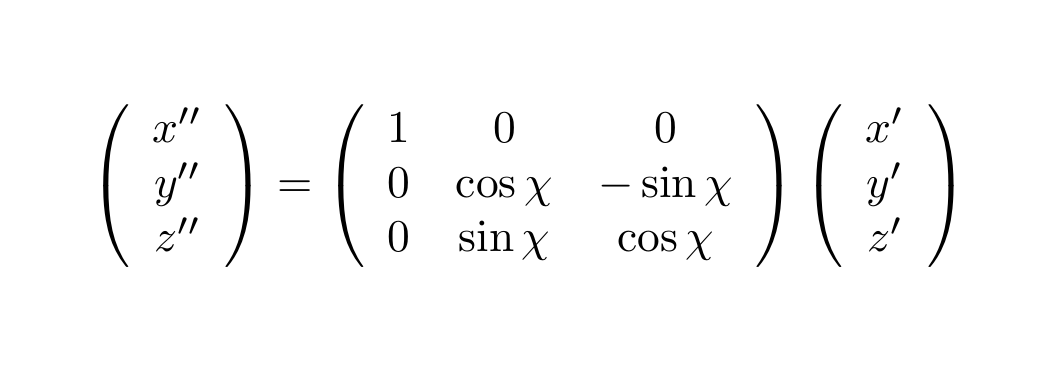
と表現できる。もう一度Z軸まわりに角度ψ回転させることで任意の方向へ回転することができる。この演算により，任意の方向を向いた単位胞のa，b，cの成分を求めることができる。

ベクトルの内積・外積に関しては

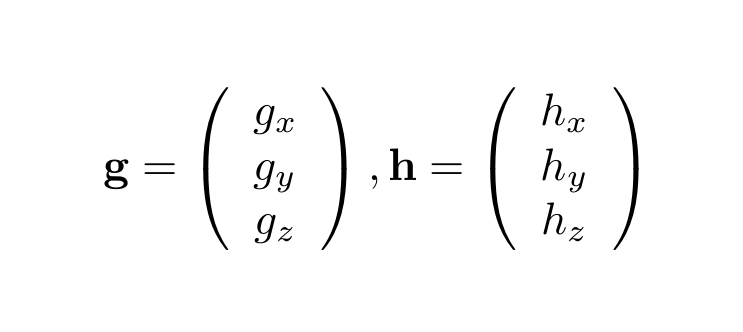
のときに

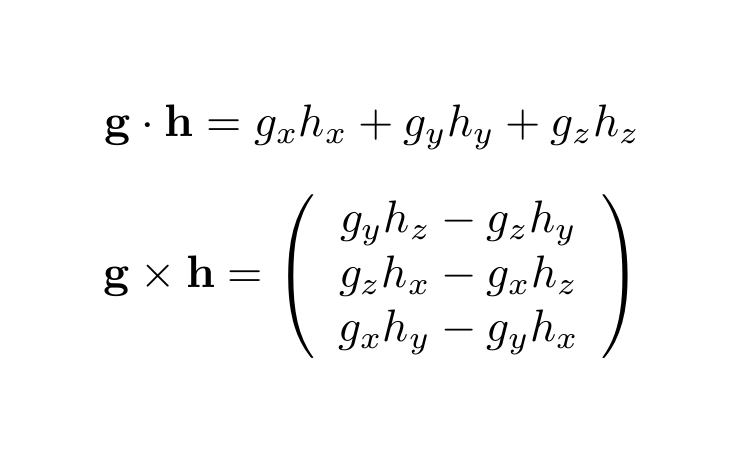
と計算できる（プログラムでは外積しか使用していないが）。

以上の式で結晶に任意の回転を与えたときの逆空間ベクトルのa^*，b^*，c^*の成分を計算できる。

回折条件の判定

回折が起こると判定するための計算式の導出を以下に記す。

• グローバル座標系のX軸を正の方向にX線が入射する。原点はO(0, 0, 0)，Ewald球の中心はP(-1.0/λ, 0, 0)とする。
• 注目する逆格子点の座標をQ(x0, y0, z0)とする。
• mosaicityによる逆格子点の広がりをωとする。
• OQがX軸となす角をξとする。

回折が起こる幾何学的な条件は逆格子点がEwald球の表面と重なることである。
故にx0=<0.0でしか回折は起こらないことは分かるので，以降はx0=<0.0の範囲で考える。
さて，点O, P, Qが乗る平面上で考える。

• r² = OQ² = x0² + y0² + z0² とする。
• R = 1.0/λとする。
• abs(x0) = -x0 = r * cos(ξ)となる。
• 点Qを平面上でω振った両端の座標をQ₁, Q₂とする。

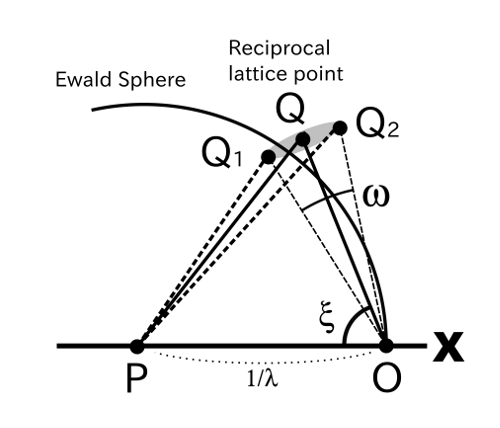
Figure: Mosaicity ω, Distance between RLPoint and center of ES

ωだけ広がった逆格子点（点？）とEwald球の表面が交差するときに回折が起こる。 これはつまりPに近い点をQ₁，遠い点をQ₂としたときに

PQ₁ =< R =< PQ₂

となれば良い。距離を求めるのに2乗の和を取ってから平方根を取るのは計算量が増えるので2乗を取るだけで済ませば良い。

PQ₁² =< R² =< PQ₂²
PQ₁² - R² =< 0
PQ₂² - R² >= 0

実際はQ₁とQ₂のどちらが近いかを調べる必要はなく，

(PQ₁² - R²) (PQ₂² - R²) =< 0

これを判定条件とする。

三角形の余弦定理(a² = b² + c² - 2bc cos A)から

PQ² = OP² + OQ² - 2* OP * OQ * cos(ξ)
PQ₁² = OP² + OQ₁² - 2* OP * OQ₁ * cos(ξ-ω/2)
PQ₂² = OP² + OQ₂² - 2* OP * OQ₂ * cos(ξ+ω/2)

PQ₁² = R² + r² - 2 * R * r * cos(ξ-ω/2)
PQ₂² = R² + r² - 2 * R * r * cos(ξ+ω/2)

PQ₁² - R² = R² + r² - 2 * R * r * cos(ξ-ω/2) - R²
= r² - 2 * R * r * (cos(ξ) * cos(ω/2) + sin(ξ) * sin(ω/2))
= r² - 2 * R * (r * cos(ξ) * cos(ω/2) + r * sqrt(1-cos²(ξ)) * sin(ω/2))
= r² - 2 * R * (r * cos(ξ) * cos(ω/2) + sqrt(r² - r² * cos²(ξ)) * sin(ω/2))
= r² - 2 * R * (abs(x0) * cos(ω/2) + sqrt(r² - x0²) * sin(ω/2))
= r² - 2 * R * (abs(x0) * cos(ω/2) + sqrt(y0² + z0²) * sin(ω/2))

PQ₂² - R² = R² + r² - 2 * R * r * cos(ξ+ω/2) - R²
= r² - 2 * R * (abs(x0) * cos(ω/2) - sqrt(y0² + z0²) * sin(ω/2))

判定条件を満たす逆格子点(h, k, l)にはflagを立てておくようにプログラムする。