高密度飼育カエルにおけるα雌の出現

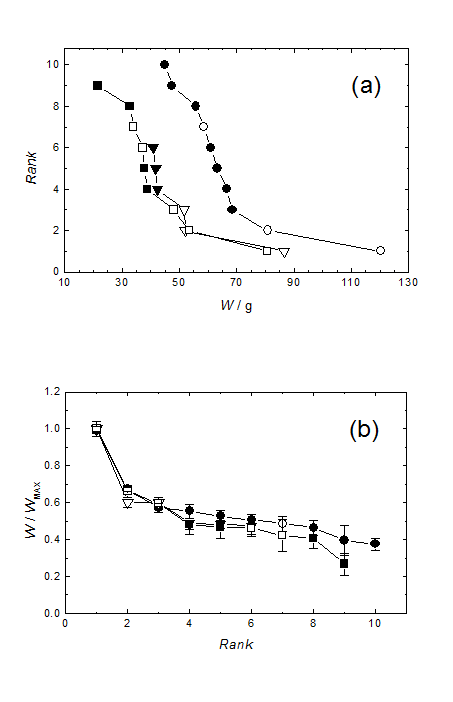
Fig. 1. Variations of (a) the frog weights (W) and (b) the relative weights (W/WMAX) in 3 incubators (circle, triangle and square symbols). Open and closed symbols indicate female and male, respectively.

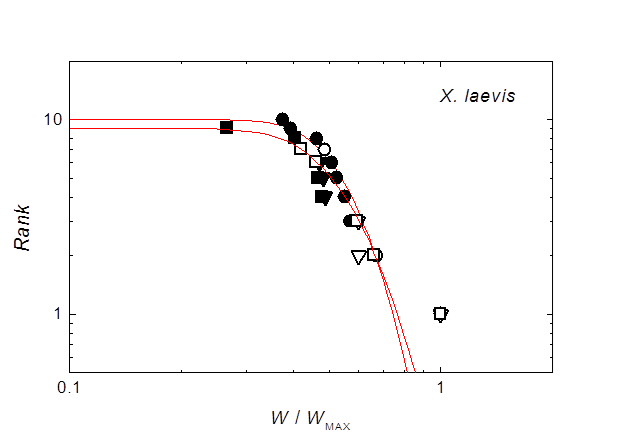
Fig. 2. Statistical analysis of the frog weights. The curves were fitted for the frogs (circles and squares) by lognormal equations.

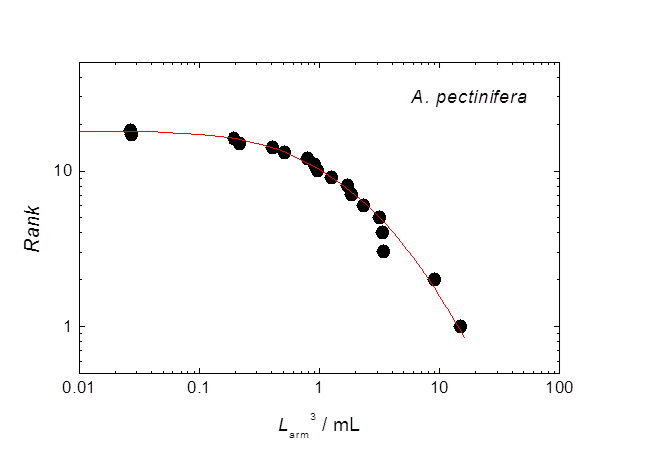
Fig. 3. Statistical analysis of the volumes (arm length)3 of the starfish, Asterina pectinifera. The curve presents a lognormal distribution.

社会的動物であるイヌ，人間を含むサル，アシナガバチなどでは，集団内の個体間に自然と序列が生まれることが知られています．皆さんも自分の所属する様々な集団ごとに，必ず序列の存在を確認できると思います．序列が約束によって決められたにせよ，あるいは自然と出来上がったにせよ，序列は集団内の衝突を回避するように働いています．しかし，同時に人間のような自我をもつ個体の集団においては，序列による衝突回避が，逆に構造的暴力の温床にもなってしまいます．このジレンマの克服は平和学の重要な課題の１つになっていますが，それはさておき，このような個体間の序列が自然に観察されるのは，社会的動物の中でも，イヌやサルのような個別個体認識がなされている社会に限られています．動物行動学では，序列のある社会で優位度の高い個体からα，β，γ．．．と呼ぶ習慣があります．社会では生殖のみならず，しばしば雄と雌の役割分担が成されていて，雌雄双方にα位が認められ，それぞれα雌，α雄と呼ばれます．

他方，アリやミツバチなどの真社会性動物では，社会に厳格な階級（カースト）が存在し，役割分担が行われています．しかし，その階級はしばしば誤解されているような力関係による序列ではありません．女王ハチは決してその名のように全体に君臨しているわけではなく，単に卵を産むことに専念しているに過ぎません．実際に，巣分かれの時には，新しい巣の場所は，探索ハチたちが民主的に協議して，コンセンサスによって決定されることが知られています．階級と序列は区別されるもののようです．

さて，社会における序列が果たしてどのように生まれたのかは，進化学，複雑系科学の観点から実に興味ある問題です．とりわけ，それに個別個体認識がどの様に関わっているかは，重要なポイントとなります．しかし，既に個別個体認識の出来上がった社会をいくら観察しても，明確な答えに行き着けるとは思えません．加えて，今ある序列社会が，何千万年もかかって進化的に形成されてきたものとするならば，その初期状態や形成経過を観察するのは不可能ということになります．この困難を克服する手立ての１つとして，実験室で社会を再構築する方法が考えられます．なかでも，自然においては社会生活を営まず，個別個体認識もない動物に，あえて人工的に集団生活をさせ，そこにどのような社会構造が生まれるかを観察する方法が考えられます．ザリガニを5匹ずつ集団生活させ，相互威嚇の観察から，5匹の間に実際に順位関係が生まれ，固定化される例がこれまでに唯一報告されています．

本研究では，実験室で受精孵化させた若齢アフリカツメカエル6から10個体を3つの水槽で高密度に飼育し，それらの成長を観察しました．カエルたちは，水槽の中でいつも互いに接触しあって生活しているのですが，ザリガニとちがって，威嚇し合うこともなく，頭を踏まれていても全く意に介さず，実に平和的な集団生活を営んでいます．餌として鶏肝が定期的に，どの個体にも十分に行渡るよう与えられるので，弱い個体が飢餓に陥るということもありません．実験室は1年中23℃に保たれているので，ちょっと混み合っていることを除けば，カエルたちは実に快適な生活を送っています．3つの水槽で飼育を始めて1年が経過し，性別も明確になったときに，水槽ごとにカエルの体重を測定した結果が，Fig. 1(a) に示されています．最大個体の体重は，最小個体の6倍に達しています．Fig. 1(b) は，各水槽の最大個体（いずれも雌）の体重を１としたときの体重比を示しています．面白いことに，水槽1と水槽3では，最大個体の体重に1.5倍もの差があるにも関わらず，体重比の変化は3つの水槽でよく一致していることが分かります．

この結果を両対数にプロットしたのがFig. 2 です．対数正規分布でフィットした結果が曲線で示されています．最大個体を除けば，曲線は実験結果をおよそ再現しています．個体が単純な確率的乗算過程で成長するときに，個体の大きさは対数正規分布になることが知られています．実際に，同一の親から生まれた兄弟稚ヒトデを1個体ずつ隔離して，十分な餌を与えて飼育すると，成長した個体には，なんと体積にして500倍ものばらつきが生まれますが，その分布は対数正規分布で表されます（Fig. 3）．したがって，体重に非常に大きな差が生まれたとしても，単一の対数正規分布になっているなら，それは社会性の結果であるとは言えません．しかし，カエルの場合，最大個体の体重だけが，対数正規分布が予測する値より３割も大きく，明らかに別格であることが分かります．また，水槽の雄がこの特別に大きな雌だけにしがみつく行動が観察されます．したがって，個別個体認識があるとは思われないカエルの高密度飼育の結果，各水槽に1頭だけ別格の優位雌，すなわちα雌が出現したことが明らかになりました．

重要なのは，社会的優位個体が，十分に餌が保障された非競争的条件の下，非敵対的集団内の自己組織化の結果として発生したことです．序列社会では，しばしば優位個体による生殖の独占が観察されます．それらは厳しい環境への適応の結果であり，生殖の独占や強固な序列が，結局最終的には種の保存に役立っていると安易に説明されてしまうことが多いのですが，今回の実験結果はむしろ，何よりもエネルギー的にゆとりのある社会であるからこそ，役割分担や序列が自己組織化される内在的条件が維持されている可能性を示しています．

（長野八久，白井浩子）