P型正20面体準結晶
Zn-Mg-RE (RE = Y, Dy, Ho, and Er)の熱容量

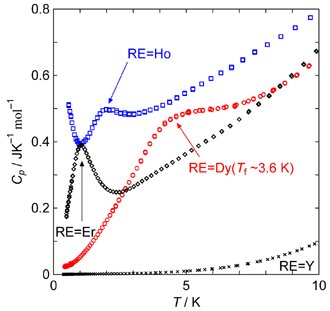
Fig. 1. Molar heat capacities of p-Zn-Mg-RE (RE = Y, Dy, Ho and Er) measured by relaxation method.

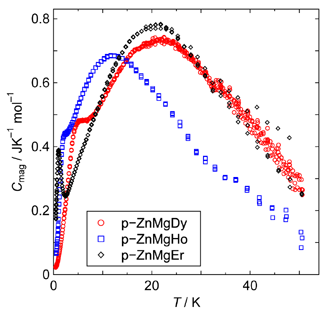Fig. 2. Magnetic specific heat contribution Cmag of p-Zn-Mg-RE (RE = Dy, Ho and Er).

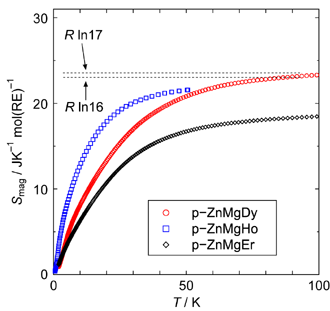Fig. 3. Magnetic entropies Smag of p-Zn-Mg-RE (RE = Dy, Ho and Er). The levels indicate the entropies expected for the respective free RE3+ ion.

Zn-Mg-RE (RE= Rare earth elements) 正20面体準結晶はその回折パターンが消滅則を示さないP型と，6次元面心格子に対応する消滅則を示すF型の2種類が知られています． 希土類元素を構造中に含むことから，準周期格子中に配置された局在4f電子による磁性という観点で関心を集めています． さらに，これらの準結晶はセンタリングの違いによる比較ができることから，また理論的にはP型準結晶において準周期長距離磁気秩序の可能性が指摘されていることからも興味がもたれています． まず先に発見されたF型準結晶（1993年）において，磁化率測定によりそのスピングラス的な振る舞いが報告されました． このF型準結晶では中性子散乱実験により，準周期長距離磁気秩序が存在しないことが確認されましたが，スピン凍結温度（Tf）以下では異方的な準周期短距離磁気秩序が発達します． これは5次元での反強磁性的スピン相関の発達として理解されています． 一方，P型準結晶は比較的最近の2002年に発見されました． 一般にF型は対応するP型準結晶のケミカルオーダーによる超格子構造と考えることができます． しかしながら，Zn-Mg-RE正20面体準結晶は，その組成がP型とF型で異なっており，問題はそう単純ではないようです． 最近の構造研究により（研究紹介8参照），P型Zn-Mg-RE準結晶はBergman型正20面体クラスターを基 本とした構造になっていることが明確になっています． 一方，磁化率測定でのスピングラス的振る舞いは，緩和時間τの増大によりスピン反転が凍結するブロッキング現象との類似も指摘されています． さらに，最近ではこれらの準結晶において絶対温度で強度がスケールできるような興味深い中性子非弾性散乱スペクトルが報告されています． これらを背景に，われわれはP型Zn-Mg-RE正20面体準結晶のRE= Y, Dy, HoおよびErの試料について極低温までの熱容量測定を行いましたのでここで紹介します．

測定に用いた試料は徐冷法により作製された多結晶（Ho試料については単結晶）です． それらを数mg程度にカットして，QUANTUM DESIGN社製PPMS Model 6000により0.4 - 300 Kの温度範囲で緩和法にて測定を行いました．それぞれの試料の組成はZn0.70Mg0.21Y0.09，Zn0.71Mg0.20Dy0.09，Zn0.75Mg0.16Ho0.09，およびZn0.75Mg0.14Y0.11です。

Dy, HoおよびErの試料では，測定温度範囲内では準周期長距離磁気秩序を示唆するような熱異常は観測されませんでした． ここでは10 K以下での熱容量CpをFig. 1に示します． 低温で大きな磁気熱容量の寄与が明らかです． Yを除くすべての試料において，スピンの凍結に対応すると思われる熱容量のピークが観測されました． 最もピーク温度が高いのはDy試料の4 Kであり，これは磁化測定の結果（Tf∼3.6 K）と対応しています． Ho試料は約2 Kにピークを示し，さらに低温では，nuclear hyperfine structureによると思われる熱容量の増大が観測されました（T < 1 K）． Er試料では約1 Kにおいて比較的大きな熱容量のピークが観測されました． Hoおよび Er試料についてはP型準結晶の磁化測定によるTfの値は不明ですが，F型準結晶ではそれぞれ1.95 Kおよび1.3 Kという値が報告されています．

Y試料については電子比熱係数γの値として0.665 mJ mol–1 K–2という小さい値が得られ，F型において報告されている値0.63 mJ mol–1 K–2と良い一致を示します． これは，Fermi面での電子の状態密度が自由電子モデルから期待される値の70%程度であり，Fermi面近傍でのpseudo gapの存在を示します．磁気熱容量を持たないY試料の格子熱容量から，Dy, HoおよびEr試料の格子熱容量を見積もり，また電子熱容量はY試料と同じと仮定して，それぞれの試料における磁気熱容量Cmagを得ました． その結果をFig. 2に示します． Dy, およびEr試料は約20 Kを中心としたブロードなピークを示します． また，Ho試料は約12 Kを中心としたブロードなピークをもつことがわかります．

次にCmagにもとづいて得られた磁気エントロピーをFig.3に示しました． Dy，HoおよびEr試料において，全角運動量JはDy3+，Ho3+およびEr3+に対する軌道およびスピン核運動量からなります． これから期待されるトータルの磁気エントロピーはRln(2J+1)から，それぞれRln16，Rln17およびRln16となります． いずれの試料においてもTf近傍では，10〜20%程度のエントロピーしか開放されません． 逆に自由な希土類イオンから期待される磁気エントロピーは50 Kよりもさらに高い温度においてやっと到達することがわかりました． これら熱容量測定の結果は，スピン凍結温度Tfからずっと離れた高温からすでに短距離的なスピン相関の発達が生じていることを示しています．

（高倉洋礼，神吉大輔）

発　表

神吉大輔，高倉洋礼，佐藤卓，稲葉章，日本物理学会2005年秋季大会（同志社大学），20aYK-8.