2次元S = 1/2三角格子化合物の
基底状態と熱励起
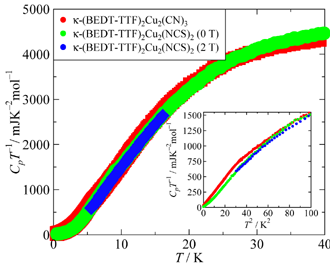 Fig. 1. Heat capacities of κ-(BEDT-TTF)2Cu2(CN)3 and κ-(BEDT-TTF)2Cu(NCS)2. Although the overall temperature dependence
of heat capacity of the two salts are similar to each other, there is a broaden hump around T2 = 25 K2 in
κ-(BEDT-TTF)2Cu2(CN)3 that is not observed in κ-(BEDT-TTF)2Cu(NCS)2.
Fig. 1. Heat capacities of κ-(BEDT-TTF)2Cu2(CN)3 and κ-(BEDT-TTF)2Cu(NCS)2. Although the overall temperature dependence
of heat capacity of the two salts are similar to each other, there is a broaden hump around T2 = 25 K2 in
κ-(BEDT-TTF)2Cu2(CN)3 that is not observed in κ-(BEDT-TTF)2Cu(NCS)2.
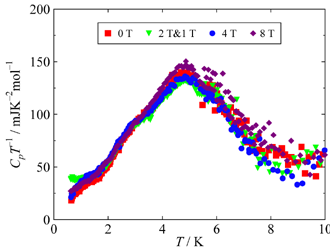 Fig. 2. The difference of CpT–1 between κ-(BEDT-TTF)2Cu(NCS)2 and κ-(BEDT-TTF)2Cu2(CN)3. The value of
magnetic entropy estimated at 10 K is about 800 mJ K–1 mol–1, which is close to 1/7 of Rln2, which value is
degeneracy of RVB state.
Fig. 2. The difference of CpT–1 between κ-(BEDT-TTF)2Cu(NCS)2 and κ-(BEDT-TTF)2Cu2(CN)3. The value of
magnetic entropy estimated at 10 K is about 800 mJ K–1 mol–1, which is close to 1/7 of Rln2, which value is
degeneracy of RVB state.
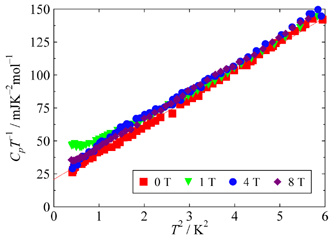 Fig. 3. Heat capacity of κ-(BEDT-TTF)2Cu2(CN)3 at low temperatures. The existence of T-linear contribution was observed.
Fig. 3. Heat capacity of κ-(BEDT-TTF)2Cu2(CN)3 at low temperatures. The existence of T-linear contribution was observed.
三角形の各頂点にスピンを配置する場合,どのように配置させても全ての隣接するスピンを反平行にすることが出来ません.
これはスピン系のフラストレーションに関する問題と呼ばれ,反強磁性相互作用が働く2次元三角格子上のS = 1/2のスピン系の基底状態は理論・実験両分野からの30年以上におよぶ研究にも関わらず未だ解明されていません.
現在,基底状態のモデルとして代表的なものとしては,それぞれのスピンが120 °ずれて配置したHeisenberg型のスピン状態が有ります.
この状態は最近接相互作用だけを考慮した場合のHamiltonianの解で,どちらかというと古典的なスピン状態に近く,統計力学的な不安定性を有しています.
もう一つの代表的なモデルであるResonating Valence Bond (RVB)状態は,次近接以降の相互作用を考慮した場合のHamiltonianの解で,どちらかというと強いスピン揺らぎをもつ量子的なスピン状態です.
格子欠陥などが無い理想的な三角格子を形成する物質がほとんど存在しなかったため,実験的な検証が難しいといわれていたフラストレーション系ですが,近年BEDT-TTFを電子提供体(ドナー)とする電荷移動塩κ-(BEDT-TTF)2Cu2(CN)3が比較的理想に近いフラストレーション系を形成することが見出されました.
この物質では,κ-(BEDT-TTF)2Cu2(CN)3の隣接サイトの相互作用の比(t/t')が1.06と1に近いこととから正三角格子に近い格子を形成し,さらにMott絶縁体であることと, BEDT-TTF2Xの持つ2次元的な電気伝導性と併せてS = 1/2の反強磁性相互作用の働く2次元三角格子スピン系を形成します.
また, κ-(BEDT-TTF)2Cu2(CN)3は低温において0.3 GPaという弱圧で超伝導状態となるため,超伝導状態とスピン状態の関係についての情報が得られることも期待されます.
今回我々は,この物質の熱容量測定を行うことによって,フラストレーション系の基底状態の解明を試みました.
Fig. 1に示したのはκ-(BEDT-TTF)2Cu2(CN)3と同型で分子量も近いκ-(BEDT-TTF)2Cu(NCS)2の熱容量の測定結果です.
10 K付近にκ-(BEDT-TTF)2Cu(NCS)2の超伝導転移に伴う熱異常が観測されていますが,この熱異常を2 Tの磁場を印加して抑制した結果,2つの塩の格子熱容量は40 Kまでのほとんどの温度域で似たような挙動を示すことがわかりました.
これより,5 K付近において見られる比較的大きな熱容量の違いは(Fig. 1),κ-(BEDT-TTF)2Cu2(CN)3に熱異常が存在すると考えられ,それぞれの塩が絶縁体と超伝導体であることから,この熱異常はスピン熱容量の差に起因するものであると考えられます.
2つの塩の熱容量の差を求めると(Fig. 2),磁場によってピークトップ温度が変化せず,また全体形状もほとんど変化がないことがわかります.
10 Kでのスピンエントロピー(約800 mJ K–1 mol–1)はS = 1/2スピンの最大エントロピー(5760 mJ K–1 mol–1)の1/7程度と比較的大きな値をとり,RVB理論で予測されている2N/4重縮退との関連が考えられます.
Fig. 3に示したκ-(BEDT-TTF)2Cu2(CN)3の低温部の熱容量では,温度に比例する項が見られます.
低温部の熱容量はサンプル依存性が見られ,熱容量が磁場依存性を持つサンプルと磁場依存性を持たないサンプルが存在しますが,いずれのサンプルでも温度に比例する項が存在し,顕著な磁場依存性もあまりありません.
今回観測された低温での比較的大きなエントロピー発生と熱容量の温度に比例する項の存在は,NMR測定による報告と同じくRVB状態の実現を示唆する結果といえます.
κ-(BEDT-TTF)2Cu2(CN)3が弱い圧力で超伝導化するという事実と熱容量測定においてRVB状態実現の兆候の関係については非常に精密な測定と議論が必要となってきます.
今後我々はκ-(BEDT-TTF)2Cu2(CN)3の物性について高磁場や超低温などさまざまな手法を用いてさらなる研究を行い,フラストレーション系の磁性状態の詳しい物性を解明することを目指しています.
(山下智史,中澤康浩)
発 表
山下智史,清水康弘,鹿野田一司,中澤康浩,小國正晴,第40回記念熱測定討論会(東京),2B0920 (2004).
山下智史,清水康弘,鹿野田一司,中澤康浩,小國正晴,日本物理学会第60回年次大会(野田),27aYL-4 (2005).
Copyright © Research Center for Structural Thermodynamics,
Graduate School of Science, Osaka University. All rights reserved.
 Fig. 1. Heat capacities of κ-(BEDT-TTF)2Cu2(CN)3 and κ-(BEDT-TTF)2Cu(NCS)2. Although the overall temperature dependence
of heat capacity of the two salts are similar to each other, there is a broaden hump around T2 = 25 K2 in
κ-(BEDT-TTF)2Cu2(CN)3 that is not observed in κ-(BEDT-TTF)2Cu(NCS)2.
Fig. 1. Heat capacities of κ-(BEDT-TTF)2Cu2(CN)3 and κ-(BEDT-TTF)2Cu(NCS)2. Although the overall temperature dependence
of heat capacity of the two salts are similar to each other, there is a broaden hump around T2 = 25 K2 in
κ-(BEDT-TTF)2Cu2(CN)3 that is not observed in κ-(BEDT-TTF)2Cu(NCS)2.
 Fig. 2. The difference of
Fig. 2. The difference of  Fig. 3. Heat capacity of κ-(BEDT-TTF)
Fig. 3. Heat capacity of κ-(BEDT-TTF)