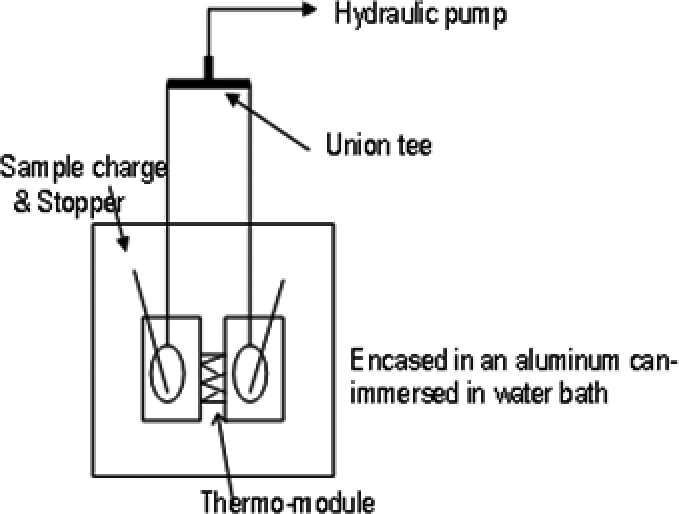
Fig. 1. Home-made apparatus.
This work is the second in our effort of determining the third derivative quantity of the Gibbs energy, G, experimentally. The first one was published elsewhere (P. Westh et al., J. Chem. Phys.129, 211101 (2008)). Prior to this, we have been evaluating third derivative quantities of G by graphically differentiating the second derivatives that have been accessible experimentally. We have thus demonstrated their power in elucidating the mixing schemes in aqueous solutions (Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, Elsevier (2007), Chapter V).
Fig. 1. Home-made apparatus.
Here we determine directly one of the third derivatives of G, the partial molar entropy-volume cross fluctuation density of 2-butoxyethanol (BE) in BE–H2O system, SVδBE. The difference of the heats of compression is directly determined between the two identical cells, on applying the same pressure change on both cells concurrently. Both cells are filled with the sample solutions with a small appropriate difference in mole fraction. For this purpose we first used Nano DSC (TA Instruments) that is designed to determine heat capacity of a sample against a reference by scanning temperature under pressure. We kept the temperature constant and changed the pressure, instead. As shown below, the statistics of the results are somewhat large probably due to the fact that the pressure perturbation is limited to 2 atm. We then home-built the apparatus capable of raising pressure change up to 100 atm. Fig. 1 shows the schematic diagram of the setup. Two identical cells with the same mass (heat capacity) and volume were filled with BE–H2O solutions with mole fraction difference ΔxBE (Δ signifies difference between two cells). The cells are connected to the hydraulic pump made of a valve filled with a low viscosity silicone oil. Pressure is changed by turning its spindle by a stepping motor. Thus a hydraulic pressure change δp (δ pertains to pressure perturbation) was applied concurrently to both cells. The difference in the heat of compression between two cells ΔδH due to pressure perturbation δp and the difference in mole fraction ΔxBE is monitored by a thermo-module.
With thermodynamic relations,
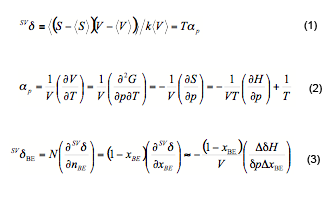
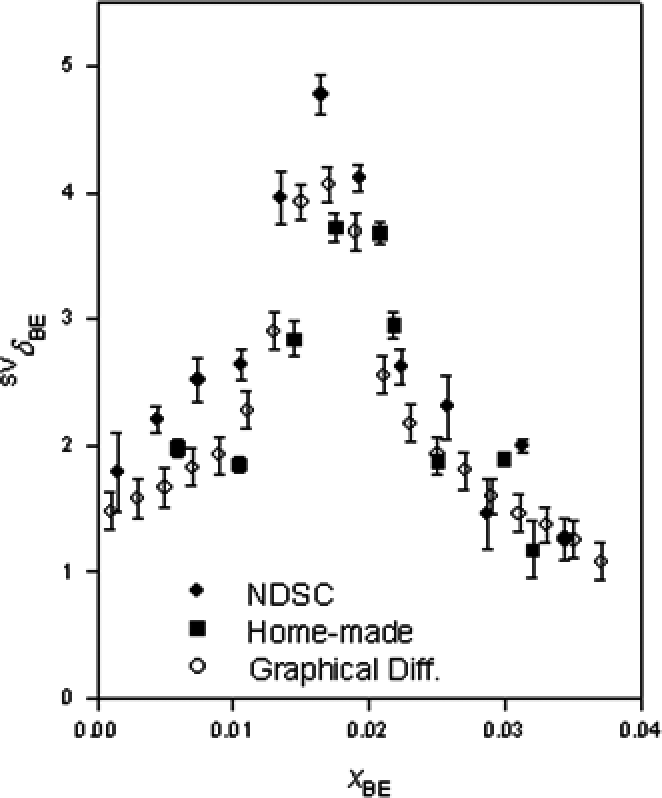Fig. 2. Results.
The results indicate that this method is feasible with the prior knowledge of the thermal expansivity data of the solution within a few per cent accuracy. If the volumes of the two cells are identical within a rather challenging 0.01%, the method provides the required results within 0.1% without the thermal expansivity data. This success opens a possibility to evaluate the fourth derivative graphically, which are expected to provide much more detailed information about the molecular processes in aqueous solutions.
Y. Koga, P. Westh, A. Inaba, K. Sou, and K. Tozaki, 45th Netsu Sokutei Touronkai, Hachioji (2009) 1B1540.
Y. Koga, P. Westh, A. Inaba, K. Sou, and K. Tozaki, J. Solution Chem. (2009) in press.