有機超伝導体 κ-(BEDT-TTF)4 Hg2.89Br8 の
熱伝導率測定

Mott絶縁性の電荷移動錯体に電子またはホールをドーピングし, 電子状態を変化をさせることは、しばしば新たな電子相への転移を促すため, 一般に興味深い物性化学研究です. 銅酸化物などの強相関系無機化合物においては, 原子置換によってドーピングが行われ, 置換比率を細かく変える事による物性の変化が詳細に研究されています. 一方, ドナー・アクセプターの2成分からなる電荷移動錯体も強い電子相互作用のせいで、非常に多様な電子物性を示すことが知られていますが, このような分子性物質では原子化学的置換によるドーピングは一般に困難です。従って、ドナー・アクセプターの比率はほとんどの場合決まった整数比しかとる事ができないため, 連続的に物性を制御することがほとんど行われておりません. 今回試料とした有機超伝導体κ–(BEDT–TTF)4Hg2.89Br8(Tc = 4.3 K)は, アニオン層中の1次元Hg鎖がドナーであるBEDT–TTFに対して不均衡な周期性を持つため, ドナー・アニオンの比率が一般的な整数比からずれており, 電荷移動錯体としては珍しくドナー層に10%程度の中途半端なホールドーピングが起きている系です. κ–(BEDT–TTF)4Hg2.89Br8は, BEDT–TTF伝導層とアニオン絶縁層が交互にスタックした構造をしており,ab面に沿って2次元的な電気伝導を示します.

0.6~150 Kの温度範囲で有機超伝導体κ–(BEDT–TTF)4Hg2.89Br8の熱伝導率を測定しました. 熱流の方向は電気伝導面内であるa軸方向です. 熱伝導率κは,
κ = kel + κph = γT + βT3 (γ,β：定数) (1)
と表すことができ, 電子熱伝導率κelはTに, 格子熱伝導率κphはT3に比例するので, 一般的に極低温では電子の寄与の方が優勢になり, ある程度以上の温度では格子の寄与の方が優勢になります. 以前に行われたκ–(BEDT–TTF)4Hg2.89Br8の電気抵抗測定の結果に対してウィーデマン-フランツ則,
κel = LTσ (L = 2.45×10-8 WΩK-2：ウィーデマン-フランツ定数) (2)
を用い, 測定を行った0.6 K以上の温度範囲における電子熱伝導率κelを見積もったところ, κel ~ 1×10-3 Wm-1K-1であり, 電子熱伝導率は全熱伝導率の1%程度と見積もられました. 測定を行った温度範囲では, 熱は主にフォノンによって伝導され, 電子の寄与は格子の寄与と比較して遥かに小さい事が分かりました.

Fig.1. Sample dependence of thermal conductivity of κ–(BEDT–TTF)4Hg2.89Br8 at low temperature.

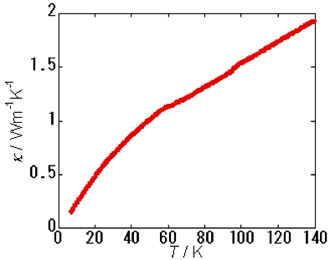Fig.2. Thermal conductivity of κ–(BEDT–TTF)4Hg2.89Br8 at low temperature.

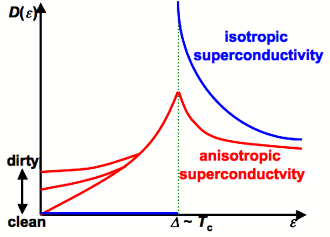Fig.3. Density of state of isotropic superconductivity and anisotropic superconductivity.

今回測定した温度範囲では, 熱伝導は主にフォノンによって担われているため, フォノン熱伝導の大きさを決定する散乱機構について考察します. まず, Fig.1に示す通り, 1~8 Kの温度範囲で, 測定した2つのκ–(BEDT–TTF)4Hg2.89Br8単結晶の熱伝導率がほとんど一致していることに注目します. 一般的に結晶中の格子欠陥の量は, 試料によってまちまちであるため, 格子欠陥がフォノンの主要な散乱機構であるとは考えにくいです. 実際, フォノンが主に格子欠陥によって散乱される場合には, 低温領域にピーク構造を伴って現れたり, 試料によって異なる熱伝導率が観測されるのが一般的ですが, Fig.2に示したより高温域での測定結果は, ピーク構造をもちません.　この結果は,低温領域において, κ–(BEDT–TTF)4Hg2.89Br8のフォノンの平均自由行程が, 格子欠陥や不純物以外の散乱原因によって支配されていることを示しており, 主に電子系によってフォノンが散乱されていると推論されます.

一方, 超伝導転移温度よりも十分低温の, 1 K以下程度の温度領域に目を転じますと, Fig.1 insetに示すように, 最大5%程度の試料依存性が現れます. 超伝導状態における準粒子の状態密度(DOS)D(ε)からこの試料依存性の起源を考察します. Fig.3に等方的なギャップをもつ等方性超伝導およびノードを含んだ異方的なギャップを有する異方性超伝導のDOSを示します. 等方性超伝導を仮定すると,T<<TcではD(ε) ~ 0であり, 準粒子はほとんど存在しないので, フォノンは欠陥や不純物などの結晶性の乱れのみによって散乱される事になり, 電子散乱が主要であるTc以上の温度領域と散乱機構が大きく異なる事になります. このことは, Fig.1で, フォノン熱伝導の温度変化がTc近辺において, 至ってスムースであることと矛盾するので, 結局κ–(BEDT–TTF)4Hg2.89Br8の超伝導ギャップは等方的ではないと考えられます. これに対して異方性超伝導は,Fig.3のようにT<<Tcにおいてエネルギーε = 0でも準粒子のDOSが存在することが知られています. 電子熱伝導率はフォノン熱伝導率と比較して十分に小さいので, ここでも準粒子は主にフォノンの散乱源として熱伝導率に影響を与えると考えられます. 異方性超伝導では, 系に欠陥や不純物などの乱れがあれば, Fig.3に示すように,ε ~ 0付近に対応する低温において, 周期性の乱れによって変化する準粒子寿命に影響を受けて低エネルギーのDOSが変化し, それに従って電子-フォノン散乱の大きさも変化します. このことから, 異方性超伝導では, 超伝導転移温度Tcより十分に低温の領域において, 欠陥・不純物の量の違いによる電子-フォノン散乱の変化を通じて熱伝導率に試料依存性が現れてよい事になります. 従って, Fig.1 insetに現れている熱伝導率の試料依存性は異方性超伝導における電子-フォノン散乱によって矛盾なく説明できます.

（岡田悠悟, 竹谷純一）